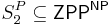S2P (complexity)

In computational complexity theory, SP
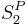2 is a complexity class. A language $L$ is in $S_2^P$ if there exists a polynomial-time predicate P such that

If 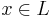$x \in L$ , then there exists a y such that for all z,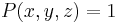 $P(x,y,z)=1$
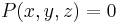
If $x \notin L$ , then there exists a z such that for all y, $P(x,y,z)=0$

where size of y and z must be polynomial of x.

1 Relations to other complexity classes
2 Karp–Lipton theorem
3 Symmetric hierarchy
4 References
5 External links

Relations to other complexity classes

Every language in NP also belongs to SP
2. For by definition, a language L is in NP, if and only if there exists a polynomial-time verifier V(x,y), such that for every x in L there exists y for which V answers true, and such that for every x not in L, V always answers false. But such a verifier can easily be transformed into an SP
2 predicate P(x,y,z) for the same language that ignores z and otherwise behaves the same as V.

More strongly, the class SP
2 contains MA (a generalization of Sipser–Lautemann theorem) and 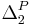$\Delta_{2}^P$ .

By definition, SP
2 is contained in 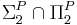$\Sigma_{2}^P \cap \Pi_{2}^P$ . Furthermore it is contained in ZPP^NP. ^[1]

Karp–Lipton theorem

A version of Karp–Lipton theorem states that if every language in NP has polynomial size circuits then the polynomial time hierarchy collapses to SP
2. This result yields a strengthening of Kannan's theorem: it is known that SP
2 is not contained in SIZE(n^k) for any fixed k.

Symmetric hierarchy

As an extension, it is possible to define 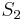$S_2$ as an operator on complexity classes; then 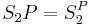$S_2 P = S_2^P$ . Iteration of 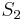$S_2$ operator yields "symmetric hierarchy".

References

^ Jin Yi-Cai. $S_2^P \subseteq \mathsf{ZPP}^{\mathsf{NP}}$ [1]

Russell Alexander, Sunaram Ravi. Symmetric Alternation captures BPP. [2]
Canetti Ran. More on BPP and the Polynomial-time Hierarchy. [3]

External links

Complexity Zoo: S₂P
Complexity Class of the Week: S₂^P, Lance Fortnow, August 28, 2002.